Two-dimensional (2D) topological insulators (TIs) are special quantum conductors that possess an insulating bulk but metallic edge with quantized charge and spin conductance protected by electron band topology. The concept of topology and TI has not only renewed our fundamental understanding of electronic properties of solid materials, but also opened an exciting avenue towards potential applications of topological quantum devices with minimized heat dissipation and robustness against disorder. In this video article, I will first introduce and review the concept of TIs within the context of transport properties of solid-state materials. I will then use two examples, the organic 2D TIs and the surface-based 2D topological states, to recap the rapid theoretical and experimental developments made in this emerging field. The existence of quantized edge conductance and topological edge states of 2D TIs has been so far confirmed experimentally in several systems, such as semiconductor quantum wells, 2D transition metal dichalcogenides, metallic overlayer of bismuth on a semiconductor surface. However, discovery of high-temperature 2D TIs and construction of functional TI-based quantum devices remain largely elusive. At the end of this video article, I will offer briefly my personal perspective and possible future directions in low-dimensional topological materials.
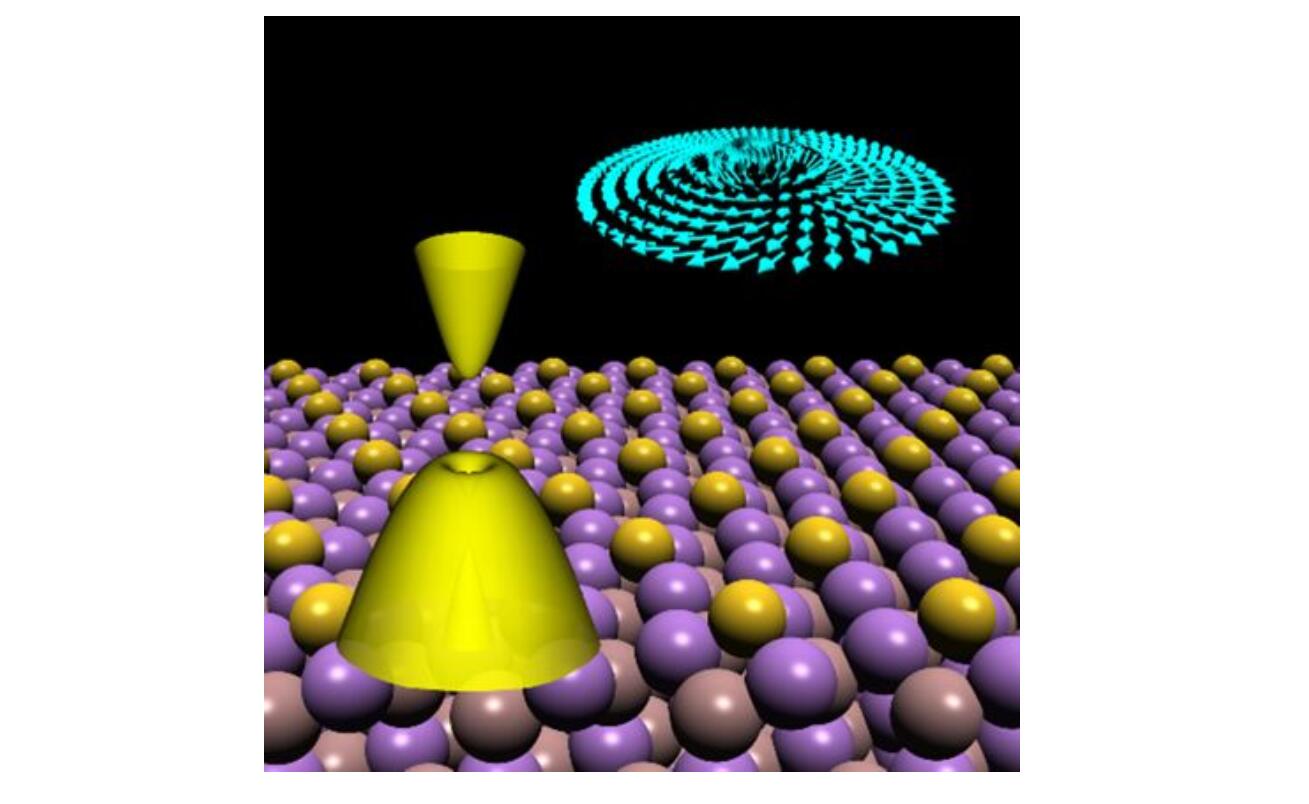
In this video review article, I will first introduce the concept of topological insulator (TI) within the context of electron transport in solid materials. In terms of electron transport, one used to classify solid materials into three different classes: metal, semiconductor, and insulator, as illustrated in Fig. 1 of slide 3 in the video article. Interestingly, TI offers a new kind of conductor with an insulating bulk but conducting boundary (edge in 2D), as a material analog of quantum Hall effect. It exhibits a zero longitudinal conductance and a quantized transverse Hall conductance defined by Chern number, as illustrated in Fig. 2 of slide 6 in the video article.
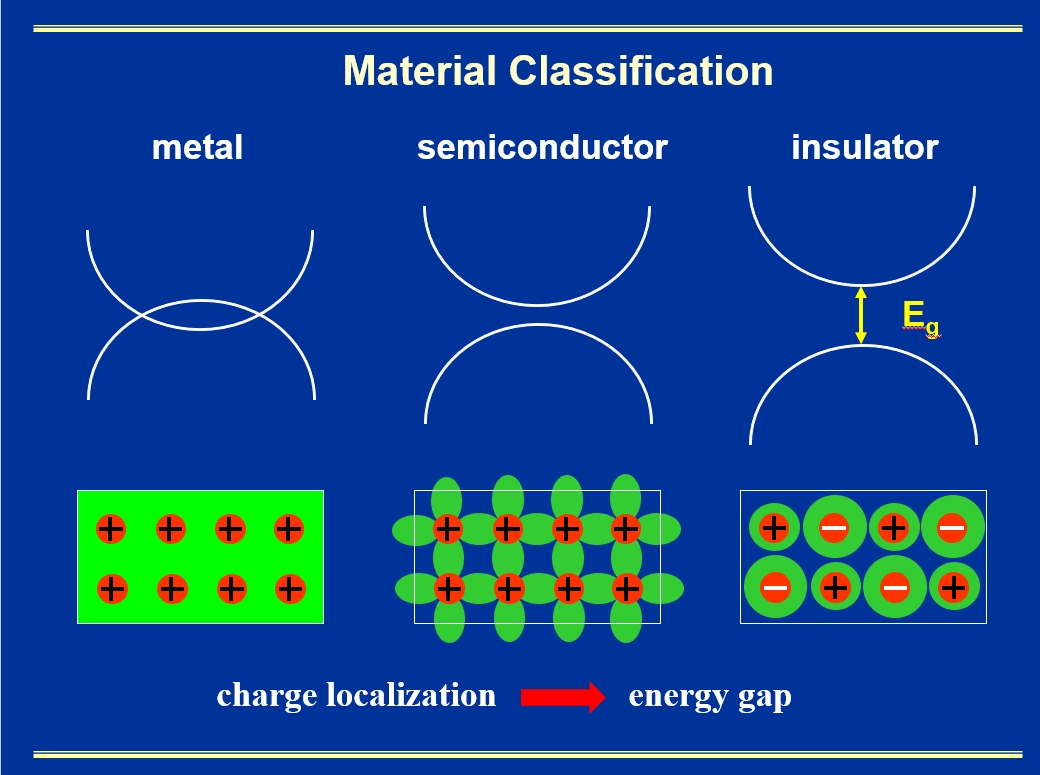
Fig. 1. A slide illustrating the band structure of metal, semiconductor and insulator, and their respective electron density distribution in real space. Note the direct correlation between charge localization in real space and band gap opening in momentum space.
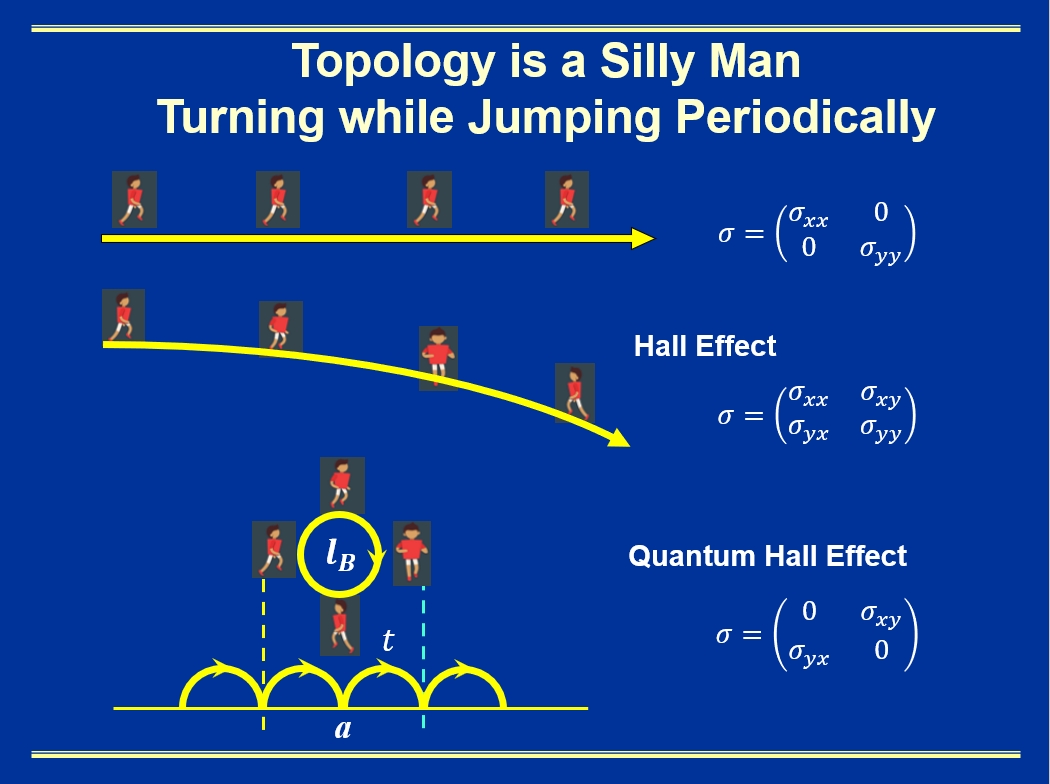
Fig. 2. A slide illustrating the analogy between TI and quantum Hall effect, in terms of conductivity tensor.
I will then review the research progress made in the 2D TIs in recent years, focusing on two systems that I am personally involved with the most. One is 2D organic TIs, and the other is the surface-based topological states, as illustrated in Fig. 3 of the slide 14 and Fig. 4 of the slide 40, respectively, in the video article.

Fig. 3. A slide highlighting three classes of 2D organic topological materials: MOFs, COFs and HOFs. The discussion in this video article will focus on MOF-based systems.

Fig. 4. A slide highlighting the idea of surface-based topological states, such as to create surface-based 2D TI by “Epitaxial Promotion of Topological States”. It means the freestanding 2D layer and substrate surface are originally trivial, but become topological after the 2D layer is grown on the substrate, as discussed in this video article.
This video article concludes with a brief summary and the author’s personal perspective on the rapidly developing fields of topological materials, as exemplified in Fig. 5 of slide 60 in the video article.
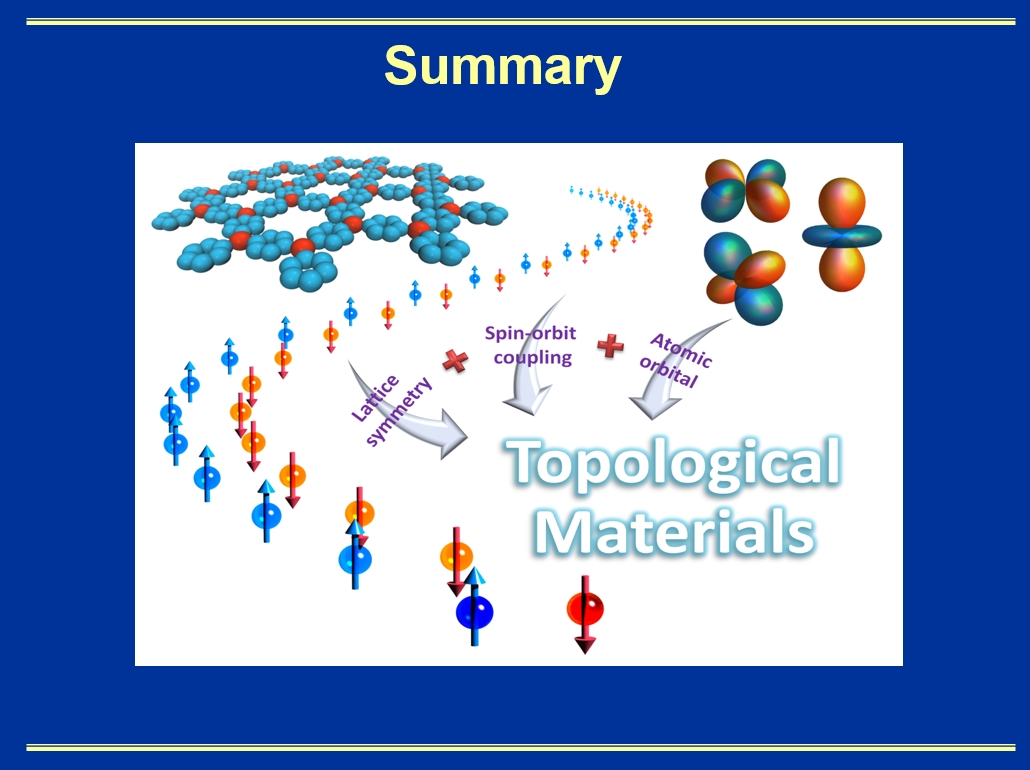
Fig. 5. A summary slide showing schematically that there are generally three ingredients in designing topological bands and materials: lattice symmetry, spin-orbit coupling, and orbital composition at the Fermi level. Many works remain to be done towards realizing topological quantum devices in the future.
Feng Liu would like to thank all the collaborators who contributed to the works reviewed in this video article. He acknowledges US Department of Energy (DOE)-Basic Energy Sciences (Grant No. DE-FG02- 04ER46148) as the primary funding support for his research group during the last two decades.
1. R.E. Prange and S.M. Girvin (Eds.), The quantum Hall effect, Springer Science & Business Media, 2012.
2. K.V. Klitzing, G. Dorda, and M. Pepper, New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance, Phys. Rev. Lett. 45, 494 (1980).
3. D.J. Thouless, M. Kohmoto, M.P. Nightingale, and M. den Nijs, Quantized Hall conductance in a two-dimensional periodic potential, Phys. Rev. Lett. 49, 405 (1982).
4. F.D.M. Haldane, Model for a quantum Hall effect without Landau levels: condensed-matter realization of the "parity anomaly", Phys. Rev. Lett. 61, 2015 (1988).
5. C.L. Kane and E.J. Mele, Quantum spin Hall effect in graphene, Phys. Rev. Lett. 95, 226801 (2005).
6. B.A. Bernevig, T.L. Hughes, and S.C. Zhang, Quantum spin Hall effect and topological phase transition in HgTe quantum wells, Science 314, 1757 (2006).
7. Z.F. Wang, K.H. Jin, and F. Liu, Quantum spin Hall phase in 2D trigonal lattice, Nat. Commun. 7, 12746 (2016).
8. M.Z. Hasan and C.L. Kane, Colloquium: topological insulators, Rev. Mod. Phys. 82, 3045 (2010).
9. X.L. Qi and S.C. Zhang, Topological insulators and superconductors, Rev. Mod. Phys. 83, 1057 (2011).
10. M. König, S. Wiedmann, C. Brüne, A. Roth, H. Buhmann, L.W. Molenkamp, X.L. Qi, and S.C. Zhang, Quantum spin Hall insulator state in HgTe quantum wells, Science 318, 766 (2007).
11. S. Murakami, Quantum spin Hall effect and enhanced magnetic response by spin-orbit coupling, Phys. Rev. Lett. 97, 236805 (2006).
12. Z. Liu, C.X. Liu, Y.S. Wu, W.H. Duan, F. Liu, and J. Wu, Stable nontrivial Z2 topology in ultrathin Bi (111) films: a first-principles study, Phys. Rev. Lett. 107, 136805 (2011).
13. T. Hirahara, G. Bihlmayer, Y. Sakamoto, M. Yamada, H. Miyazaki, S. Kimura, S. Blügel, and S. Hasegawa, Interfacing 2D and 3D topological insulators: Bi(111) bilayer on Bi2Te3, Phys. Rev. Lett. 107, 166801 (2011).
14. F. Yang, L. Miao, Z.F. Wang, M.Y. Yao, F.F. Zhu, Y.R. Song, M.X. Wang, J.P. Xu, A.V. Fedorov, Z. Sun, G.B. Zhang, C.H. Liu, F. Liu, D. Qian, C.L. Gao, and J.F. Jia, Spatial and energy distribution of topological edge states in single Bi(111) bilayer, Phys. Rev. Lett. 109, 016801 (2012).
15. X. Zhang, H.J. Zhang, J. Wang, C. Felser, and S.C. Zhang, Actinide topological insulator materials with strong interaction, Science 335, 1464 (2012).
16. D. Hsieh, D. Qian, L. Wray, Y. Xia, Y.S. Hor, R.J. Cava, and M.Z. Hasan, A topological Dirac insulator in a quantum spin Hall phase, Nature 452, 970 (2008).
17. Y. Xia, D. Qian, D. Hsieh, L. Wray, A. Pal, H. Lin, A. Bansil, D. Grauer, Y.S. Hor, R.J. Cava, and M.Z. Hasan, Observation of a large-gap topological-insulator class with a single Dirac cone on the surface, Nat. Phys. 5, 398 (2009).
18. H.J. Zhang, C.X. Liu, X.L. Qi, X. Dai, Z. Fang, and S.C. Zhang, Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface, Nat. Phys. 5, 438 (2009).
19. Y.L. Chen, J.G. Analytis, J.H. Chu, Z.K. Liu, S.K. Mo, X.L. Qi, H.J. Zhang, D.H. Lu, X. Dai, Z. Fang, S.C. Zhang, I.R. Fisher, Z. Hussain, and Z.X. Shen, Experimental realization of a three-dimensional topological insulator, Bi2Te3, Science 325, 178 (2009).
20. H. Lin, R.S. Markiewicz, L.A. Wray, L. Fu, M.Z. Hasan, and A. Bansil, Single-Dirac-cone topological surface states in the TlBiSe2 class of topological semiconductors, Phys. Rev. Lett. 105, 036404 (2010).
21. Y.L. Chen, Z.K. Liu, J.G. Analytis, J.H. Chu, H.J. Zhang, B.H. Yan, S.K. Mo, R.G. Moore, D.H. Lu, I.R. Fisher, S.C. Zhang, Z. Hussain, and Z.X. Shen, Single Dirac cone topological surface state and unusual thermoelectric property of compounds from a new topological insulator family, Phys. Rev. Lett. 105, 266401 (2010).
22. S. Souma, K. Eto, M. Nomura, K. Nakayama, T. Sato, T. Takahashi, K. Segawa, and Y. Ando, Topological surface states in lead-based ternary telluride Pb(Bi1−xSbx)2Te4, Phys. Rev. Lett. 108, 116801 (2012).
23. D. Xiao, Y. Yao, W.X. Feng, J. Wen, W.G. Zhu, X.Q. Chen, G.M. Stocks, and Z.Z. Zhang, Half-Heusler compounds as a new class of three-dimensional topological insulators, Phys. Rev. Lett. 105, 096404 (2010).
24. H. Lin, L.A. Wray, Y.Q. Xia, S.Y. Xu, S. Jia, R.J. Cava, A. Bansil, and M. Z. Hasan, Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena, Nat. Mater. 9, 546 (2010).
25. S. Chadov, X.L. Qi, J. Kübler, G.H. Fecher, C. Felser, and S.C. Zhang, Tunable multifunctional topological insulators in ternary Heusler compounds, Nat. Mater. 9, 541 (2010).
26. Z.F. Wang, Z. Liu, and F. Liu, Organic topological insulators in organometallic lattices, Nat. Commun, 4, 1471 (2013).
27. C.X. Liu, X.L. Qi, X. Dai, Z. Fang, and S.C. Zhang, Quantum anomalous Hall effect in Hg1−yMnyTe quantum wells, Phys. Rev. Lett. 101, 146802(2008).
28. Z.H. Qiao, S.A. Yang, W.X. Feng, W.K. Tse, J. Ding, Y.G. Yao, J. Wang, and Q. Niu, Quantum anomalous Hall effect in graphene from Rashba and exchange effects, Phys. Rev. B 82, 161414(R) (2010).
29. H.B. Zhang, C. Lazo, S. Blügel, S. Heinze, and Y. Mokrousov, Electrically tunable quantum anomalous Hall effect in graphene decorated by 5d transition-metal adatoms, Phys. Rev. Lett. 108, 056802 (2012).
30. R. Yu, W. Zhang, H.J. Zhang, S.C. Zhang, X. Dai, and Z. Fang, Quantized anomalous Hall effect in magnetic topological insulators, Science 329, 61 (2010).
31. C.Z. Chang, J.S. Zhang, X. Feng, J. Shen, Z.C. Zhang, M.H. Guo, K. Li, Y.B. Ou, P. Wei, L.L. Wang, Z.Q. Ji, Y. Feng, S.H. Ji, X. Chen, J.F. Jia, X. D, Z. Fang, S.C. Zhang, K. He, Y.Y. Wang, L. Lu, X.C. Ma, and Q.K. Xue, Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator, Science 340, 167 (2013).
32. Z.F. Wang, Z. Liu, and F. Liu, Quantum anomalous Hall effect in 2D organic topological insulators, Phys. Rev. Lett. 110, 196801 (2013).
33. Z. Liu, Z.F. Wang, J.W. Mei, Y.S. Wu, and F. Liu, Flat Chern band in a two-dimensional organometallic framework, Phys. Rev. Lett. 110, 106804 (2013).
34. Z.F. Wang, N.H. Su, and F. Liu, Prediction of a two-dimensional organic topological insulator, Nano Lett. 13, 2842 (2013).
35. M.H. Pan, X. Zhang, Y.N. Zhou, P.D. Wang, Q. Bian, H. Liu, X.Y Wang, X.Y. Li, A.X. Chen, X.X. Lei, S.J. Li, Z.W. Cheng, Z.B. Shao, H.X. Ding, J.Z. Gao, F.S. Li, and F. Liu, Growth of mesoscale ordered two-dimensional hydrogen-bond organic framework with the observation of flat band, Phys. Rev. Lett. 130, 036203 (2023).
36. M. Zhou, W.M. Ming, Z. Liu, Z.F. Wang, P. Li, and F. Liu, Epitaxial growth of large-gap quantum spin Hall insulator on semiconductor surface, Proc. Natl. Acad. Sci. 111, 14378 (2014).
37. Q.Y. Wang, Z. Li, W.H. Zhang, Z.C. Zhang, J.S. Zhang, W. Li, H. Ding, Y.B. Ou, P. Deng, K. Chang, J. Wen, C.L. Song, K. He, J.F. Jia, S.H. Ji, Y.Y. Wang, L.L. Wang, X. Chen, X.C. Ma, and Q.K. Xue, Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3, Chin. Phys. Lett. 29, 037402 (2012).
38. Z.F. Wang, H. Zhang, D. Liu, C. Liu, C. Tang, C. Song, Y. Zhong, J. Peng, F. Li, C. Nie, L. Wang, X.J. Zhou, X. Ma, Q.K. Xue, and F. Liu, Topological edge states in a high-temperature superconductor FeSe/SrTiO3(001) film, Nat. Mater. 15, 968 (2016).
39. Z.F. Wang and F. Liu, Self-assembled Si(111) surface states: 2D Dirac material for THz plasmonics, Phys. Rev. Lett. 115, 026803 (2015).
40. M. Zhou, W.M. Ming, Z. Liu, Z.F. Wang, Y.G. Yao, and F. Liu, Formation of quantum spin Hall state on Si surface and energy gap scaling with strength of spin orbit coupling, Sci. Rep. 4, 7102 (2014).
41. Z.G. Song, C.C. Liu, J.B. Yang, J.Z. Han, M. Ye, B.T. Fu, Y.C. Yang, Q. Niu, J. Lu, and Y.G. Yao, Quantum spin Hall insulators and quantum valley Hall insulators of BiX/SbX (X=H, F, Cl and Br) monolayers with a record bulk band gap, NPG Asia Materials 6, e147 (2014).
42. Y.D. Ma, Y. Dai, L.Z. Kou, T. Frauenheim, and T. Heine, Robust two-dimensional topological insulators in methyl-functionalized bismuth, antimony, and lead bilayer films, Nano Lett. 15, 1083 (2015).
43. L. Li, X. Zhang, X. Chen, and M. Zhao, Giant topological nontrivial band gaps in chloridized gallium bismuthide, Nano Lett. 15, 1296 (2015).
44. C.J. Wu and S.D. Sarma, px,y-orbital counterpart of graphene: cold atoms in the honeycomb optical lattice, Phys. Rev. B 77, 235107 (2008).
45. G.F. Zhang, Y. Li, and C.J. Wu, Honeycomb lattice with multiorbital structure: topological and quantum anomalous Hall insulators with large gaps, Phys. Rev. B 90, 075114 (2014).
46. F. Reis, G. Li, L. Dudy, M. Bauernfeind, S. Glass, W. Hanke, R. Thomale, J. Schäfer, and R. Claessen, Bismuthene on a SiC substrate: a candidate for a high-temperature quantum spin Hall material, Science 357, 287 (2017).
47. M. Zhou, Z. Liu, W.M. Ming, Z.F. Wang, and F. Liu, sd2 graphene: kagome band in a hexagonal lattice, Phys. Rev. Lett. 113, 236802 (2014).
48. H.Q. Huang and F. Liu, A unified view of topological phase transition in band theory, Research, 2020, ID 7832610.
49. C.X. Liu, T.L. Hughes, X.L. Qi, K. Wang, and S.C. Zhang, Quantum spin Hall effect in inverted type-II semiconductors, Phys. Rev. Lett. 100, 236601 (2008).
50. I. Knez, R.R. Du, and G. Sullivan, Evidence for helical rdge modes in inverted InAs/GaSb quantum wells, Phys. Rev. Lett. 107, 136603 (2011).
51. L.J. Du, I. Knez, G. Sullivan, and R.R. Du, Robust helical edge transport in gated InAs/GaSb bilayers, Phys. Rev. Lett. 114, 096802 (2015).
52. X.F. Qian, J.W. Liu, L. Fu, and J. Li, Quantum spin Hall effect in two-dimensional transition metal dichalcogenides, Science 346, 1344 (2014).
53. S.J. Tang, C.F. Zhang, D. Wong, Z. Pedramrazi, H.Z. Tsai, C.J. Jia, B. Moritz, M. Claassen, H. Ryu, S. Kahn, J. Jiang, H. Yan, M. Hashimoto, D.H. Lu, R.G. Moore, C.C. Hwang, C. Hwang, Z. Hussain, Y.L. Chen, M.M. Ugeda, Z. Liu, X.M. Xie, T.P. Devereaux, M.F. Crommie, S.K. Mo, and Z.X. Shen, Quantum spin Hall state in monolayer 1T'-WTe2, Nat. Phys. 13, 683 (2017).
54. S.F. Wu, V. Fatemi, Q.D. Gibson, K. Watanabe, T. Taniguchi, R.J. Cava, and P.J. Herrero, Observation of the quantum spin Hall effect up to 100 kelvin in a monolayer crystal, Science 359, 76 (2018).
55. S.K. Chong, L.Z. Liu, K. Watanabe, T. Taniguchi, T.D. Sparks, F. Liu, and V.V. Deshpande, Emergent helical edge states in a hybridized three-dimensional topological insulator, Nat. Commun. 13, 6386 (2022).
56. Y.F. Ren, Z.H. Qiao, and Q. Niu, Topological phases in two-dimensional materials: a review, Rep. Prog. Phys. 79, 066501 (2016).
57. Z.F. Wang, K.H. Jin, and F. Liu, Computational design of two-dimensional topological materials, WIREs Comput. Mol. Sci., e1304 (2017).
58. W. Jiang, X.J. Ni, and F. Liu, Exotic topological bands and quantum states in metal–organic and covalent–organic frameworks, Acc. Chem. Res. 54, 416 (2021).
59. H.Q. Huang and F. Liu, Quantum spin Hall effect and spin Bott index in a quasicrystal lattice, Phys. Rev. Lett. 121, 126401(2018).
60. C.T. Wang, T. Cheng, Z.R. Liu, F. Liu, and H.Q. Huang, Structural amorphization-induced topological order, Phys. Rev. Lett. 128, 056401 (2022).
Comment #1 by reviewer:
On slide 9, there is a statement “Quantum spin Hall effect can be viewed as a two copies of QAHE”. Since the concept of QAHE is not mentioned before this slide, the audience may not be able to understand what it means. QSHE could also be described as two superimposed quantum Hall effects under opposite magnetic fields. It might be easier to describe this with a cartoon.
Author’s response:
Thanks for this comment. The concept of QAHE is introduced earlier in slide 7 discussing Haldane’s model of Chern insulator by inserting a Berry flux into a hexagon of a hexagonal lattice. In slide 8, Kane-Mele model of QSHE is discussed by adding the SOC effect in a hexagonal lattice which effectively inserts one Berry flux in each spin channel in opposite direction. In this sense, one can see that “QSHE can be viewed as two copies of QAHE”. Or at the referee put it that QSHE can also be described by two superimposed QHE under opposite magnetic field.
Comment #2 by reviewer:
When the AFM quantum spin Hall effect in FeSe monolayer was discussed, both AFM and FM edge states were mentioned. I am confused about these concepts. Here more discussions should be given. I also couldn’t follow the discussions which indicate the predicted AFM QSHI is supported by the STS data. Since there are much data presented in that slide, it would be helpful to the audience if Prof. Liu could point out which specific data provides key evidence for the AFM QSHI.
Author’s response:
Thanks for this comment. In slide 37, Figure b indicates the AFM edges are along the diagonal direction, while the FM edges are along the x- and y-direction. In a conventional QSH insulator, the dispersion of topological edge states is usually independent of edge orientation. However, due to different magnetic order, the dispersion of topological edge stages of AFM QSH insulator is different along the AFM versus FM edge, which were shown in slide 38 by theoretical calculations. This interesting difference in topological edge states can be used as a unique signature to experimentally detect an AFM QSH insulator, which was shown in slide 39 where the integrated edge states around the bulk topological gap for AFM versus FM edges are compared between theory and experimental STS measurements, showing very good agreement.
Comment #3 by reviewer:
At one slide, Prof. Liu mentioned “magnetic translation” and “flux translation". What do they refer to? Clear definitions should be given for these concepts.
Author’s response:
Thanks for this comment. As mentioned in the response to comment #2, in Haldane’s model of Chern insulator, a Berry flux is imagined to be inserted into a hexagon of a hexagonal lattice, and by translation symmetry, one can view this flux is periodically translated over the infinite lattice, namely the “flux translation”. Similarly, in the classical QHE experiment, a strong perpendicular magnetic field is applied to a 2D electron gas inducing a magnetic flux. Topology arises when the magnetic length (or the radius of magnetic flux) is comparable with the underlying lattice constant, giving rise to a strong interplay between “magnetic translation” and lattice “translation”, as illustrated in slide 5.
Comment #4 by reviewer:
Near the end of presentation, Prof. Liu pointed out that TI can be present even in amorphous materials or liquid. It would be useful to the audience if some possible examples could be given.
Author’s response:
Thanks for this comment. One specific example of amorphous 2D TI is theoretically predicted in amorphous stanane, a hydrogenated monolayer α-Sn [Wang et. al., Phys. Rev. Lett. 128, 056401 (2022)], awaiting for experimental confirmation.



